VOLUME BENDA PUTAR
DENGAN POROS PUTAR GARIS y = k, DAN GARIS x = h
(Materi Pengayaan)
Standar Kompetensi
Menggunakan konsep integral dalam pemecahan masalah.
Kompetensi Dasar
Menggunakan integral untuk menghitung luas daerah di bawah kurva dan volum benda putar
Tujuan Pembelajaran
Setelah mempelajari materi peserta didik diharapkan mampu:
- Melakukan transformasi masalah menghitung volume benda putar dengan poros putar garis y = k, dan x = h ke masalah menghitung volume benda putar dengan poros putar sumbu X, dan sumbu Y
- Menghitung volume benda putar apabila daerah yang dibatasi oleh dua kurva di putar terhadap garis y = k.
- Menghitung volume benda putar apabila daerah yang dibatasi oleh dua kurva di putar terhadap garis x = h.
Introduksi
Bagaimana yach caranya menghitung volume benda putar apabila sumbu putarnya bukan sumbu-sumbu koordinat, tetapi garis yang sejajar sumbu X atau garis yang sejajar sumbu Y? sepertinya sulit yaaaach. Jawabnya, bisa menjadi mudah seperti menghitung volume benda putar dengan poros putar sumbu X atau sumbu Y. Mengapa bisa demikian? Ya…a…a karena memang bisa… mau tahu caranya? Kalo mau terusin baca …
Ada sedikit materi prasyarat sebelum ke materi pokok. Dalam geometri transformasi ada yang dinamakan dengan Translasi atau pergeseran dinyatakan dengan .
a adalah bilangan real yang menyatakan jauhnya pergeseran searah sumbu X, jika a negatif pergeseran sejauh a ke kiri, dan jika a positif pergeseran sejauh a ke kanan.
b adalah bilangan real yang menyatakan jauhnya pergeseran searah sumbu Y, jika b negatif pergeseran sejauh b ke bawah, dan jika b positif pergeseran sejauh b ke atas.
Contoh:
Titik A(2, 5) oleh translasi "7, -1" digeser ke titik B(9, 4)
Garis y = 2x + 1 oleh translasi "7, -1" digeser ke garis atau persamaan barunya menjadi
y – (-1) = 2(x – 7) +1 disederhanakan menjadi y = 2x - 14
Rumus Umum
Ilustrasi
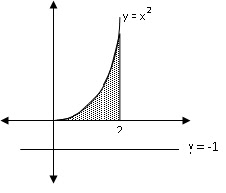
Misalnya daerah yang dibatasi oleh kurva y = x2, garis x = 2, dan sumbu X diputar mengelilingi garis y = - 1, bagaimana caranya ngitung volume benda putar yang terjadi?
Biar gak bingung mudah-mudahan banyak membantu, daerah yang dimaksud klo digambar kayak berikut,
Jadi daerah yang diarsir diputar mengelilingi garis y = - 1 (bukan mengelilingi sumbu X).
Sebetulnya terdapat lebih dari satu cara untuk menyelesaikan masalah tersebut, tetapi cara yang akan dibahas pada tulisan ini adalah mentrasformasi masalah baru ini ke masalah yang telah akrab dengan kalian.
Peta pikirannya adalah sbb,
- Pertamax
Poros putar dalam hal ini garis y = - 1 kita geser/translasi sejauh 1 satuan searah sumbu Y ke atas supaya berimpit dengan sumbu X, hal ini menjadi dasar untuk menentukan komponen translasi (berhenti dulu 1 menit biar aman deh …).
Komponen translasi tersebut ditulis sebagai artinya:
Searah sumbu X kita tidak melakukan pergeseran baik ke kiri maupun ke kanan sehingga komponen pertama dinyatakan dengan 0
Searah sumbu Y kita melakukan persgeseran ke atas sejauh 1 satuan sehingga komponen kedua dinyatakan dengan 1
Begitulah ceritanya seperti kata materi prasyarat di atas.
Berhenti lagi untuk diendapkan ….pokonya setiap hal yang memerlukan pengendapan berhenti dulu … ok.
- Keduax
Akibatnya atau konsequensinya semua batas daerah yang diputar harus digeser sejauh 1 satuan ke atas, rinciannya:
- Sumbu X digeser 1 satuan ke atas menjadi garis y = 1
- Kurva y = x2 digeser 1 satuan ke atas menjadi y – 1 = x2
Þ y = x2 + 1
- Garis x = 2 digeser 1 satuan ke atas persamaan baru tetap x = 2
- Ketigax
Masalah di atas sudah siap untuk ditransfromasi ke masalah yang akrab dengan kalian, perhatikan table berikut:
Masalah Menghitung Vol. Benda Putar Dengan Poros Putar garis y = - 1 | Masalah Menghitung Vol. Benda Putar Dengan Poros Putar Sumbu X |
Daerah yang dibatasi oleh kurva y = x2, garis x = 2, dan sumbu X diputar mengelilingi garis y = - 1. Hitunglah volume benda putar yang terjadi. | Daerah yang dibatasi oleh kurva y = x2 + 1, garis x = 2, dan garis y = 1 diputar mengelilingi sumbu X. Hitunglah volume benda putar yang terjadi. |
Jadi untuk menyelesaikan soal pada kolom kiri sama dengan menyelesaikan soal pada kolom kanan. Penyelesaiannya? Terserah Anda ….
Pada kasus volume benda putar dengan poros putar garis x = h yaitu garis-garis yang sejajar sumbu Y, cara penyelesaiannya analogi dengan kasus volume benda putar dengan poros putar garis y = k. Sebagai dasar translasi adalah jauhnya pergeseran garis x = h agar berimpit dengan sumbu Y. Proses yang dilakukan adalah transfromasi
masalah
volume benda putar dengan poros putar garis x = h
ke masalah
volume benda putar dengan poros putar sumbu Y.
Contoh:
Daerah yang dibatasi oleh garis y = x + 2 , sumbu X, dan sumbu Y diputar mengelilingi garis X = 1. Hitunglah volume benda putar yang terjadi.
Agar garis x = 1 berimpit dengan sumbu Y, harus dilakukan pergeseran 1 satuan ke kiri atau translasi
, maka hasil lengkapnya sebagai berikut:
, maka hasil lengkapnya sebagai berikut:
| Kondisi Asal | Kondisi Hasil Translasi |
| Garis x = 1 | Sumbu Y |
| Garis y = x + 2 | Garis y = x + 3 (dari y – 0 = (x - -1) + 2) |
| Sumbu X | Sumbu X |
| Sumbu Y | Garis x = - 1 |
| Daerah yang dibatasi oleh garis y = x + 2 , sumbu X, dan sumbu Y diputar mengelilingi garis X = 1. Hitunglah volume benda putar yang terjadi. | Daerah yang dibatasi oleh garis y = x + 3, sumbu X, dan garis x = - 1 diputar mengelilingi sumbu Y. Hitunglah volume benda putar yang terjadi. |
| Penyelesaian Volume benda putar yang terjadi adalah: | |
Latihan
Daerah D dibatasi oleh kurva dan garis x = 2y.
Hitung volume benda putar yang terjadi, jika daerah D diputar terhadap :
(1) sumbu x
(2) garis x = -1
(3) garis y = 4
(4) sumbu y
(5) garis y = -2
(6) garis x = 4
(4) sumbu y
(5) garis y = -2
(6) garis x = 4









-_-
BalasHapusWah, terima kasih Pak! Sangat berguna buat saya yang mau UAS, penjelasannya mudah dimengerti. :D
BalasHapusTerima kasih pak, sangat membantu..
BalasHapusTp bagaimana kalau d putar melalu garis y=x apakah harus d rotasi?
Terimakasih bapak
BalasHapus